ALJABAR BOOLEAN

- Dalam matematika dan ilmu komputer, Aljabar Boolean adalah struktur aljabar yang "mencakup intisari" operasi logika AND, OR, NOR, dan NAND dan juga teori himpunanuntuk operasi union, interseksi dan komplemen.

- Penamaan Aljabar Boolean sendiri berasal dari nama seorang matematikawan asal Inggris, bernama George Boole. Dialah yang pertama kali mendefinisikan istilah itu sebagai bagian dari sistem logika pada pertengahan abad ke-19.

- Boolean adalah suatu tipe data yang hanya mempunyai dua nilai. Yaitu true atau false (benar atau salah).

- Pada beberapa bahasa pemograman nilai true bisa digantikan 1 dan nilai false digantikan 0.

- Ada beberapa gerbang yang harus kita pelajari dalam Aljabar Boolean,yaitu :

• GERBANG DASAR – NOT

Penyangkalan dengan kata-kata "Tidak" (NOT) 1≠0  dan  0≠1.Yang artinya 1 tidak sama dengan 0,dan 0 tidak sama dengan 1.

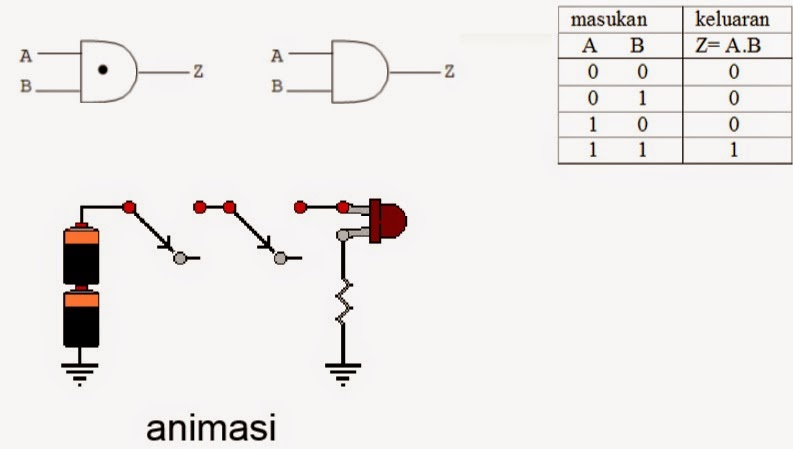
• GERBANG DASAR – AND

AND :    Z = A.B = AB

Artinya,Nilai Keluaran(Z) sama dengan nilai dari perkalian masukannya(A.B)(AB).

• GERBANG DASAR – OR

OR :    Z = A+B

Artibnya,Nilai keluarannya sama dengan nilai tambah dari masukannya(A+B).

• GERBANG TAMBAHAN

Ø  GERBANG NOR

Gerbang ini adalah kebalikan dari gerbang sebelumnya,yakni Gerbang OR.Rumus dari gerbang ini adalah =

NOR : Z ≠ (A+B)

Ø  GERBANG NAND

Gerbang ini adalah kebalikan dari gerbang sebelumnya,yakni Gerbang AND.Rumus dari gerbang ini adalah =

NAND : Z ≠ (AB)

Ø  Gerbang EXOR

Disini,bila nilai masukannya bernilai sama maka akan memberi nilai keluaran False(0).Tapi bila nilai masukannya mempunyai nilai yg berbeda maka akan memberi nilai keluaran True(1).

Rumusnya =

• ·        TEOREMA DASAR ALBOOLEAN

• ·        TEOREMA TAMBAHAN BOOLEAN

• ·        PENYAJIAN FUNGSI BOOLEAN

a.      Suku­min(singkatan dari "suku minimum" minterm, minimum term)

~ Sum Of Product, nilai 1

b.      sukumax (singkatan dari "suku maksimum" maxterm, maximum term)

~ Product of sum, nilai 0

CONTOH :

• ·        FUNGSI TIDAK LENGKAP

~  ‘d’ (dont care), dapat dianggap 1 ataupun0 tergantung pertimbangan desain

~ Contoh : y =  m (0,3,7) +  d (1,6)

PETA KARNAOUGH

- Digunakan untuk menyederhanakan fungsi boolean

- Dengan cara memetakan tabel kebenaran dalam kotak-kotak segi empat yang jumlahnya tergantung dari jumlah peubah (variabel) masukan

- Penyederhanaan untuk setiap “1” yang bertetanggaan 2,4,8,16… menjadi suku minterm yang sederhana

- Meskipun aljabar Boole merupakan suatu sarana untuk menyederhanakan pernyataan logika, belum dapat dipastikan bahwa pernyataan yang disederhanakan dengan aljabar Boole itu merupakan pernyataan yang paling sederhana.

- Prosedur meminimumkan agak sulit dirumuskan karena tidak adanya aturan yang jelas untuk menentukan langkah manipulasinya.

- Metode peta karnaugh memberikan suatu prosedur yang mudah

#Format K-Map

- n variabel input akan menghasilkan 2n kombinasi minterm yang diwakili dalam bentuk segiempat (kotak).

- Peta Karnaugh 2 variabel memerlukan 22 atau 4 kotak, peta karnaugh 3 variabel mempunyai 23 atau 8 kotak, dst

Contoh K-Map 2 Variabel :

Contoh K-Map 3 Variabel :

- Peletakan posisi suku minterm

Contoh : f = S m (0,1,2,4,6)

Contoh K-Map 4 Variabel :

- Peletakan posisi suku minterm

Contoh : f = S m (0,2,8,10,12,14 )

Contoh K-Map 5 Variabel :

- Peletakan posisi suku minterm

Contoh : f = S m (0,7,8,15,16,23,24)

Peta Karnaugh 6 Variabel
- Peletakan posisi suku minterm

Contoh :

f = S m (0,4,10,11,18,21,22,23,26,27,29,30,31,32,36,50, 53,54,55,58,61,62,63)

#Peta Karnaugh maxterm

- Dengan cara memetakan tabel kebenaran dalam kotak-kotak segi empat yang jumlahnya tergantung dari jumlah peubah (variabel) masukan

- Penyederhanaan untuk setiap “0” yang bertetanggaan 2,4,8,16… menjadi suku maxterm yang sederhana.

Contoh : g = p M(1,3,4,5,6,7,9,11,13,15)

- Peta Karnaugh dapat digunakan untuk menilik kesamaan dua buah fungsi boolean

Contoh : Buktikan kesamaan